
QUÂN TƯỢNG
Xét bàn cờ vuông kích thước \(n \times n\). Các dòng được đánh số từ 1 đến \(n\), từ dưới lên trên. Các cột được đánh số từ 1 đến \(n\) từ trái qua phải.
Ô nằm trên giao của dòng \(i\) và cột \(j\) được gọi là ô \((i,j)\). Trên bàn cờ có \(m\ (0\ \leq \ m\ \leq \ n)\) quân cờ. Với \(m\ > \ 0\), quân cờ thứ \(i\) ở ô \((r_{i},\ c_{i}),\ i\ = \ 1,2,...,\ m\). Không có hai quân cờ nào ở trên cùng một ô. Trong số các ô còn lại của bàn cờ, tại ô \((p,\ q)\) có một quân tượng. Mỗi một nước đi, từ vị trí đang đứng quân tượng chỉ có thể di chuyển đến được những ô trên cùng đường chéo với nó mà trên đường đi không phải qua các ô đã có quân
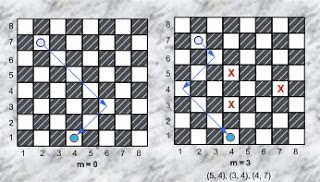
Cần phải đưa quân tượng từ ô xuất phát \((p,\ q)\) về ô đích \((s,t)\). Giả thiết là ở ô đích không có quân cờ. Nếu ngoài quân tượng không có quân nào khác trên bàn cờ thì chỉ có 2 trường hợp: hoặc là không thể tới được ô đích, hoặc là tới được sau không quá 2 nước đi (hình trái). Khi trên bàn cờ còn có các quân cờ khác, vấn đề sẽ không còn đơn giản như vậy.
Yêu cầu: Cho kích thước bàn cờ \(n\), số quân cờ hiện có trên bàn cờ \(m\) và vị trí của chúng, ô xuất phát và ô đích của quân tượng. Hãy xác định số nước đi ít nhất cần thực hiện để đưa quân tượng về ô đích hoặc đưa ra số -1 nếu điều này không thể thực hiện được.
Dữ liệu vào:
+ Dòng đầu tiên chứa 6 số nguyên \(n,\ m,\ p,\ q,\ s,\ t\).
+ Nếu \(m\ > \ 0\) thì mỗi dòng thứ \(i\) trong \(m\) dòng tiếp theo chứa một cặp số nguyên \(r_{i}\) , \(c_{i}\) xác định vị trí quân thứ \(i\).
Hai số liên tiếp trên cùng một dòng được ghi cách nhau ít nhất một dấu cách.
Dữ liệu ra:
Gồm 1 dòng duy nhất là số nước đi tìm được
Ví dụ:
| Input | Output |
|---|---|
| 8 3 7 2 1 4 5 4 3 4 4 7 | 3 |
Hạn chế:
Trong tất cả các test: \(1\ \leq \ n\ \leq \ 200\). Có 60% số lượng test với \(n\ \leq \ 20\).
Bạn cần đăng nhập để nộp bài
| Code tích cực |
|---|
| Trong 24h |
|
| Trong 7 ngày |
| Trong 30 ngày |
|
| Kỳ thi |
|---|
| Lập trình cơ bản |
| Luyện thi Chuyên Tin - CB |
| Luyện thi Chuyên Tin - NC |
| Tuyển tập Đề thi Tuyển sinh 10 |
| Tuyển tập Đề thi HSG THCS |
| Tuyển tập Đề thi HSG THPT |
| Tuyển tập Đề thi HSG Chọn đội tuyển |
| Thống kê |
|---|
|
AC/Sub: 120817/226949 Pascal: 18142 C++: 157988 Python: 50747 Lượt xem/tải tests: 42171 |
