
DOMINO
Domino (domino.*)
Bờm và Cuội gần đây đã tìm thấy một bảng trò chơi xếp hình domino cổ đại. Bảng có hình dạng chữ nhật được chia thành các lưới ô vuông kích thước \(n \times m\), các hàng được đánh số từ 1 đến \(n\), các cột được đánh số từ 1 đếm \(m\), và \(n\) và \(m\) là các số tự nhiên lẻ. Bảng được lấp đầy bởi \(\frac{n \times m - 1}{2}\) quân domino, mỗi domino chiếm hai ô liền kề, một số domino được đặt theo chiều ngang, một số lại được đặt theo chiều dọc và rõ ràng sẽ có một ô trên bảng không bị quân domino nào đặt lên.
Bờm và Cuội nhìn vào bảng này và nghĩ về tất cả những nhiệm vụ tuyệt với có thể nghĩ ra từ bảng xếp hình domino này. Một ý tưởng ngay lập tức nảy ra với họ. Với cách đặt các ô domino trên một bảng hiện tại, thì có thể di chuyển được bao nhiêu quân domino từ vị trí ban đầu của chúng đến vị trí khác, hay có bao nhiêu quan có thể thay đổi vị trí?
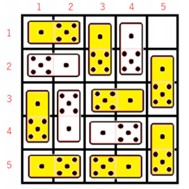
Ví dụ, đối với một bảng được sắp xếp như trên, ô trống ở vị trí (1,5), trước tiên chúng ta có thể di chuyển domino đặt trên các ô (2,5), (3,5) lên trên và do đó, ô trống sẽ là ô (3,5). Sau khi di chuyển nó, ta có thể di chuyển domino pr các ô (4,5), (5,5) lên trên hoặc domino ở (3,3), (3,4) về phía phải. Trong tổng số 12 quân cờ domino trên bảng này, tám quân trong đó có thể được di chuyển khỏi vị trí ban đầu của chúng theo một cách nào đó.
Hãy viết một chương trình đếm xem có bao nhiêu quân cờ domino khác nhau có thể được di chuyển được ra vị trí khác theo một cách nào đó.
Dữ liệu vào:
+ Dòng đầu tiên chứa hai số nguyên \(n\) và \(m\) là số hàng và số cột của bảng, cả hai đều là các số lẻ \((1 \leq n,m < 500)\).
+ Dòng thứ \(i\) trong \(\frac{(n \times m - 1)}{2}\) tiếp theo, mỗi dòng chứa bốn số nguyên dương \(x_{1},y_{1},x_{2},y_{2}\) tương ứng là vị trí đặt quân domino thứ \(i\) trên bảng là hai ô \(\left( x_{1},y_{1} \right)\) và \(\left( x_{2},y_{2} \right)\) với \(x_{1},x_{2}\) là chỉ số hàng và \(y_{1},y_{2}\) là chỉ số cột. Dữ liệu đảm bảo các quân domino không xếp chồng lên nhau, không vượt quá giới hạn của bảng, hai ô của một quân domino đặt lên là hai ô kề nhau trên bảng.
Kết quả: Ghi ra một số nguyên duy nhất là số quân domino có thể di chuyển ra vị trí khác với vị trí ban đầu.
Ví dụ:
| Input | Output |
|---|---|
| 5 5 4 3 4 4 4 5 5 5 5 2 5 1 1 2 1 1 3 4 3 3 5 4 5 3 4 1 3 1 3 2 4 2 2 3 1 3 2 5 3 5 1 4 2 4 2 1 2 2 | 8 |
Ràng buộc:
+ Subtask 1: 45% số điểm có \(1 \leq n,m \leq 5\);
+ Subtask 2: 25% số điểm có \(n = m = 9\) và tối đa có 2 quân domino có thể di chuyển;
+ Subtask 3: 30% số điểm còn lại không có ràng buộc gì thêm.
Bạn cần đăng nhập để nộp bài
| Code tích cực |
|---|
| Trong 24h |
|
| Trong 7 ngày |
| Trong 30 ngày |
|
| Kỳ thi |
|---|
| Lập trình cơ bản |
| Luyện thi Chuyên Tin - CB |
| Luyện thi Chuyên Tin - NC |
| Tuyển tập Đề thi Tuyển sinh 10 |
| Tuyển tập Đề thi HSG THCS |
| Tuyển tập Đề thi HSG THPT |
| Tuyển tập Đề thi HSG Chọn đội tuyển |
| Thống kê |
|---|
|
AC/Sub: 120817/226949 Pascal: 18142 C++: 157988 Python: 50747 Lượt xem/tải tests: 42171 |
