
SIMULATION
Simulation (simulation.*)
Bờm đang lập trình cho một cánh tay robot để có thể dùng phấn vẽ lên trên bảng đen, coi bảng đen là một mặt phẳng tọa độ chuẩn Oxy (trục Ox tăng từ trái sang phải, trục Oy tăng từ dưới lên trên).
Kế hoạch mô tả các thao tác thực hiện của cánh tay robot là một mảng gồm \(n\) vector (\(x_{1},y_{1}\)), (\(x_{2},\ y_{2}\)), ..., (\(x_{n},y_{n}\)), trong đó \(x_{i}\) và \(y_{i}\) là các số nguyên chẵn. Vận hành thực tế của cánh tay robot như sau: đầu tiên nó bắt đầu đặt viên phấn từ điểm (1, 1) và sau đó thực hiện \(n\) bước, ở bước thứ \(i\), cánh tay robot sẽ di chuyển viên phấn trên bảng từ điểm hiện tại (\(x,\ y\)) đến thẳng điểm (\(x + x_{i},\ y + y_{i}\)). Ta có thể hình dung cánh tay robot đang vẽ một loại đường đứt đoạn trong mặt phẳng tọa độ, và các đoạn của đường đứt đoạn đó chính là các vector đã cho.
Trong khi Bờm đang nghĩ về cách thay đổi kế hoạch để thay đổi đường đứt đoạn mà robot có thể vẽ ra, anh ấy tự hỏi viên phấn sẽ đi qua các trục tọa độ bao nhiêu lần với đường robot sẽ vẽ ra với kế hoạch hiện tại. Do đó Bờm muốn có một chương trình mô phỏng quá trình thay đổi kế hoạch và trả lời các truy vấn số lần đi qua trục tọa độ với đường robot vẽ ra, để anh ấy có thể dễ dàng tùy chỉnh kế hoạch cho robot theo ý mình.
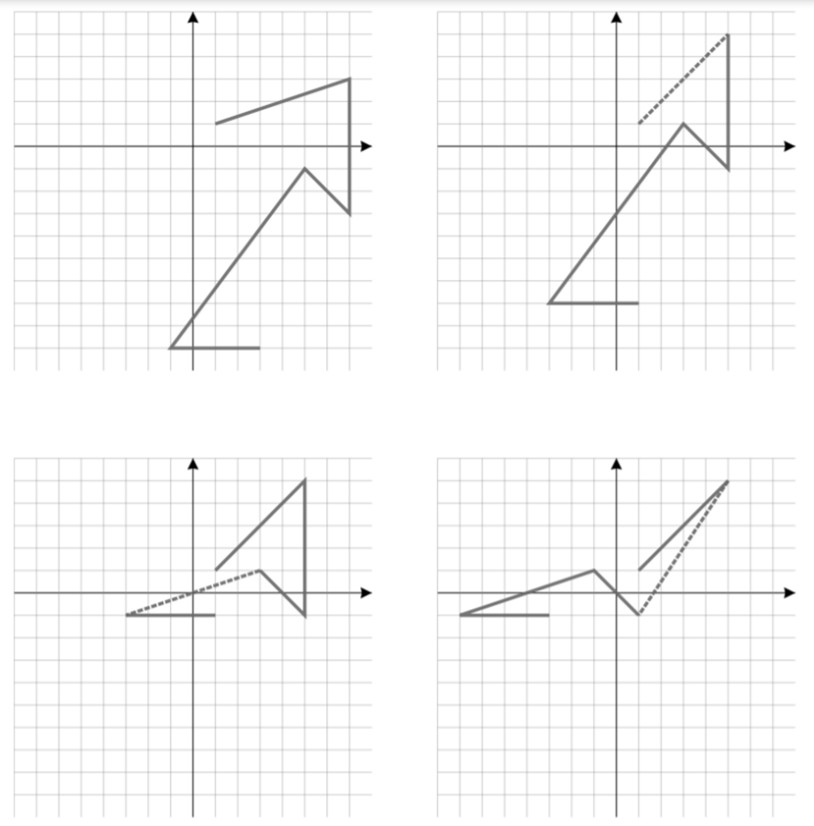
Giả sử kế hoạch mô tả các thao tác của robot chứa \(n\) vector là một mảng đánh số từ 1 đến \(n\). Ban đầu con trỏ của chương trình mô phỏng chỉ vào vị trí 1 của mảng này. Và chương trình mô phỏng cần thực hiện các lệnh sau:
“\(\mathbf{B}\)”: lùi con trỏ về vị trí trước vị trí hiện tại trong mảng (nếu vị trí hiện tại là \(i\) thì nó sẽ lùi về vị trí \(i - 1\), nếu \(i = 1\) thì nó giữ nguyên vị trí hiện tại).
“\(\mathbf{F}\)”: di chuyển con trỏ đến vị trí tiếp theo trong mảng (nếu vị trí hiện tại là \(i\) thì nó sẽ tiến đến vị trí \(i + 1\), nếu \(i = n\) thì nó giữ nguyên vị trí hiện tại).
“\(\mathbf{C\ }\mathbf{n}_{\mathbf{x}}\mathbf{\ }\mathbf{n}_{\mathbf{y}}\)”: thay đổi vector của vị trí hiện tại của con trỏ trong mảng thành (\(n_{x},\ n_{y}\)), với \(n_{x},\ n_{y}\) cũng là những số nguyên chẵn.
“\(\mathbf{Q}\)”: trả lời câu hỏi của Bờm rằng với kế hoạch hiện tại thì đường robot sẽ vẽ ra có bao nhiêu lần đi qua trục tọa độ. Nếu đi qua gốc (0, 0) thì được tính là 2 lần đi qua trục tọa độ.
Yêu cầu: hãy xây dựng chương trình mô phỏng nêu trên.
Dữ liệu vào:
Dòng đầu tiên chứa số nguyên \(n\) (\(1 \leq n \leq 10^{5}\))
Tiếp theo là \(n\) dòng, mỗi dòng chứa hai số nguyên \(x_{i}\) và \(y_{i}\) (\(\left| x_{i} \right|,\ \left| y_{i} \right| \leq 500\))
Dòng tiếp theo chứa số nguyên \(m\) là số thao tác truy vấn (\(1 \leq m \leq 3 \times 10^{5}\))
Tiếp theo là \(m\) dòng, mỗi dòng mô tả một trong 4 truy vấn trên (\(\left| n_{x} \right|,\ \left| n_{y} \right| \leq 500\)).
Kết quả: Ghi ra nhiều dòng, mỗi dòng ứng với kết quả của truy vấn loại “\(q\)”.
Ví dụ:
| Input | Output |
|---|---|
| 5 6 2 0 -6 -2 2 -6 -8 4 0 12 Q C 4 4 Q F F F C -6 -2 Q B B C -4 -6 Q | 3 5 5 4 |
Chú ý:
Có 30% số điểm có \(n,\ m \leq 1000\)
Có 30% số điểm có \(y_{i} = n_{y} = 0,\ n \leq 5 \times 10^{4},\ m \leq 10^{5}\)
Có 20% số điểm có \(n \leq 5 \times 10^{4},\ m \leq 10^{5}\)
Có 20% số điểm còn lại không có ràng buộc gì thêm.
Bạn cần đăng nhập để nộp bài
| Code tích cực |
|---|
| Trong 24h |
|
| Trong 7 ngày |
| Trong 30 ngày |
|
| Kỳ thi |
|---|
| Lập trình cơ bản |
| Luyện thi Chuyên Tin - CB |
| Luyện thi Chuyên Tin - NC |
| Tuyển tập Đề thi Tuyển sinh 10 |
| Tuyển tập Đề thi HSG THCS |
| Tuyển tập Đề thi HSG THPT |
| Tuyển tập Đề thi HSG Chọn đội tuyển |
| Thống kê |
|---|
|
AC/Sub: 120817/226949 Pascal: 18142 C++: 157988 Python: 50747 Lượt xem/tải tests: 42171 |
